The Argument for Problem Solving First

In a well-controlled experiment published in 2019, a pair of Harvard physicists showed that students who engaged in active instruction had significantly higher performance on a test of learning than those who were engaged in passive instruction. However, students did not feel as though they were learning with active instruction and preferred passive instruction.

The results of this study encourages us to consider the idea of active instruction for our own classes, even if our students may be resistant. But what is active learning? When should it be used? And how do we make this approach work for our students?

Summary of the 2019 study

The scientist in me loves the design of the 2019 study. Harvard University students enrolled in an introductory physics class were randomly chosen to engage in active learning versus passive lectures for one topic and then switched the learning approach for a second topic. The two topics were static equilibrium and fluids – both of which involve mathematics-based problems. Many variables were kept constant, like the handouts, the instructors who stayed with the groups, and the tests that were not designed by the instructors. Scientifically, this study is so well controlled that the results can be considered a true measure of the learning. 

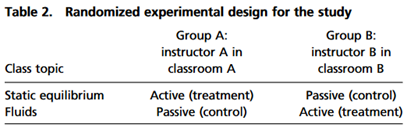
The article describes active instruction as students solving sample problems in small groups with the instructor offering support where needed before being told how to solve the problems. With passive instruction, the students were told how to solve the problems before practicing solving problems on their own or in small groups. Looking at other literature in this field, we can equate ‘active instruction’ with problem solving followed by instruction (PS-I) approach to teaching. 

Evidence for PS-I Approach

Many of you reading this blog may be thinking “but I teach mathematics to non-Harvard students, how does this apply to my teaching?” We will address the similarities and differences with this study later. First, we will explore an article published in 2017 that analyzed twenty published studies comparing PS-I and I-PS, most of them using mathematics content like variability or math-intensive science content like average speed and density. 

The authors were looking for qualities of the problem solving stage and the instruction stage that could be most beneficial for student learning, so they broke down the studies into those where the problem solving stage used contrasting cases or rich problems and whether the instruction stage was built upon students’ solutions or not. The learning outcomes (assessments) of the different studies were grouped into procedural (how to solve), conceptual (understanding through reasoning or connecting), or transfer (application to new situation or problem). 

When contrasting cases were used in the problem solving phase, regardless of whether the instruction built on student solutions or not, there was a positive effect on student’s learning of conceptual outcomes or transfer outcomes. When rich problems followed by instruction that built upon student solutions was used, students performed better when assessed for conceptual understandings or transfer. The results measuring procedural knowledge was mixed (Table 2). 

Recall that each of the studies in this article compared the PS-I approach with the more traditional instruction followed by problem solving approach (I-PS). The results of the Loibl, et. al. 2017 study demonstrate that a PS-I approach is effective for learning concepts and for students being able to transfer knowledge and that there are qualities of a PS-I approach that are more favorable than others to advance student learning. 

Table 2: Summary of “Table 3: Classification of studies and summary of learning outcomes” from Loibl, et. al. (2017).

* Total number of studies does not equal 20 because two articles included two different studies.

Why is PS-1 Effective?

The Loibl, et. al. 2017 study used the results of their analysis to identify reasons why PS-I is effective. The main reason? Problem-solving-first activates prior knowledge. When students are presented with a problem that is unfamiliar, they have to tap into what they already know - in cognitive terms, they activate their existing schema. Once activated, students are able to fit new knowledge into that schema. Without that prior activation, students may see the knowledge being shared during the instruction phase as something new, trying to create a new schema rather than incorporating into existing schemas. 

The idea of activating prior knowledge as a reason for the effectiveness of PS-I is supported by some of the findings. PS-I as an approach does not appear to be effective with young students (grades 2-5). Many of these students do not yet have complex schemas to activate as they have had little exposure to concepts like equivalence. If students are asked to evaluate existing erroneous solutions to problems, they may activate some prior knowledge, but asking students to construct their own solutions shows increased knowledge gain. Likely because they have to activate more of their own knowledge. 

Another reason PS-I works is that students can become aware of their knowledge gaps. When attempting to solve unfamiliar problems, it is likely that they may fail to find an acceptable solution. With subsequent instruction, especially instruction based upon students’ solutions, then students can become aware of their own knowledge gaps. They can then use the new knowledge to fill in those gaps, strengthening their existing schemas. 

These reasons may explain why PS-I is not always effective when the desired outcome is procedural knowledge. Often with procedural knowledge, students do not have prior experience to activate. I took a class with an award-winning instructor on how to use R statistical software. The instructor provided active direct instruction with students engaging in the program as he explained the procedures. This I-PS approach was very effective as the learning objectives were procedural rather than conceptual.   

Students’ Attitude Towards PS-1

As outlined above, the evidence from multiple studies supports the idea that PS-I is an effective approach for promoting students’ concept and transfer knowledge. However, there was an additional finding from the 2019 Harvard study that we need to address. While students did learn more with a PS-I approach, students felt like they learned more with the passive I-PS approach. 

After each learning experience, students not only took a test of learning, they were also asked their opinions of their learning on a survey. There were significant differences in students’ attitudes favoring a passive or I-PS approach to learning on items like “Instructor was effective at teaching” and “I feel like a learned a great deal from this lecture.” In follow-up interviews, students said the PS-I class did not flow well and they felt frustrated and confused. The authors summarize these finding as “novice students are poor at judging their actual learning and thus rely on inaccurate meta-cognitive cues such as fluency of instruction.”

In short, students don’t like the PS-I approach and don’t believe they are learning. However, in a follow-up study instructors presented the results of this study demonstrating that students did indeed learn more with a problem-solving first approach. At the end of the semester, where a PS-I approach was used more often, “65% of students reported on a survey that their feelings about the effectiveness of active learning significantly improved over the course of the semester.” Having students be aware that PS-I is effective for learning may improve students’ attitudes with the approach. 

Implementing in the Math Classroom

In implementing lessons learned from these articles in our own classrooms, we need to keep in mind some of the unique features. First, most of the content taught with the PS-I approach was math-intensive science concepts or statistics. The numbers used represent variables, so there is a built-in practical component, linking content and concepts with observable phenomena. If we want to use the PS-I approach, we need to have problems that can connect to real world phenomena, so even if students struggle with the mathematics, they can still activate their prior knowledge on a real-world experience. 

Second, the students in the 2019 study were taking physics at Harvard University. This means that the students had been successful in school settings that usually use more passive forms of instruction. They were also either majoring in science or had enough of a mathematical background so as to feel comfortable taking a physics class. This population of students may have been more resistant to a PS-I approach because it was new to them and they had demonstrated success with passive I-PS learning.

What do these features mean for our classrooms? First, consider your content. Are the concepts you are teaching transferable to real world phenomena? Then find good problems that can be used to activate students’ prior knowledge. If you have access, ModernMath has practical non-Googleable problems and activities like Graphs in the World for different math content that can be used immediately in your classroom. 

Second, consider your students. With students who have struggled with traditional schooling, there may be less resistance and more acceptance of the PS-I approach, especially if it were explained first that this approach is effective at improving learning. Improved learning aside, allowing students to work in small groups solving problems lets students get to know one another, building a classroom community, which is beneficial for students’ learning.

 Take Aways:

• A problem-solving first approach (PS-I) improves learning for older students in math courses over a passive, instruction-first (I-PS) approach. 

• Allowing students to struggle with problems initially taps into their prior knowledge and may make them aware of knowledge gaps, improving their learning. 

• Students may not like a PS-I approach and may not think they are learning. Share with them the evidence from these studies demonstrating that this approach is effective for learning.