To Flip or Not to Flip the Math Classroom

The flipped classroom has become a popular teaching model with the potential to engage students in active learning and increase student outcomes. But what does the research say about the effectiveness of the flipped classroom? Does it improve student outcomes, and if so, what aspects of the model promote the observed positive change? 

The article “The Flipped Classroom in Introductory Statistics: Early Evidence from a Systematic Review and Meta-Analysis” compares flipped and traditional classroom models across multiple published studies. Results of the article, confounding issues, and further implications for flipping your own introductory undergraduate math courses are addressed in this blog.

Definition of Flipped Classroom

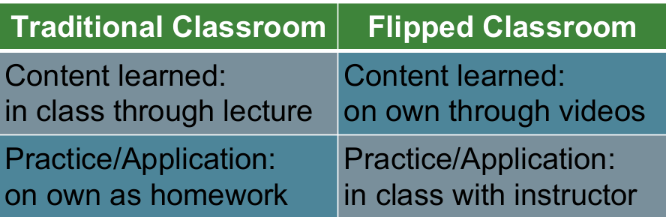
The flipped classroom is a blended learning model where students first access content online, generally through video lectures, prior to an in person class meeting. This allows for class time to be spent in practicing and applying content with peer and instructor support. Passive lecture-based learning can be done outside of class on the students’ own time, maximizing student participation and engagement during class. 

This model is called the ‘flipped’ classroom to contrast with a traditional classroom where students access content during a scheduled in person lecture and then engage in practice or application of content on their own as homework. The differences between the two models is in where and with whom the students access content and then practice or apply content.

There appear to be some clear advantages to using a flipped classroom. The students have the lectures readily available online, allowing them to access the content as needed. If a student is struggling with practice or application of the content, then peer and instructor support are available during class time.

Introductory statistics is a good candidate for using the flipped classroom model. With the dependence on math vocabulary, students could first learn the terms and concepts in a video lecture. This allows for time during class to address difficult concepts and apply the vocabulary appropriately. 

Article Review

The article described in this blog analyzed eleven published studies of undergraduate introductory statistics courses, each with a quasi-experimental design comparing student learning outcomes from a flipped classroom and a traditional lecture class. The narrowness of the selected studies allowed for clear comparison of the two models and for identification of factors that influence student performance outcomes. Each included study compared exam grades or final course grades and could be represented as percentages with standard deviations. The commonalities in outcomes as percentages for the studies allowed for robust statistical analysis and ease of combining and comparing the different studies.

Nine of eleven studies showed a statistically significant higher average performance in the flipped classroom than in the traditional lecture class. One study did not have a significant difference and the other showed a higher performance in the traditional classroom over the flipped classroom. The results of the latter study could be explained by content exposure time with the traditional classroom having 3 hours of in-person class a week and the flipped classroom having only 1 hour per week of in-class time (Gundlach, E., et.al., 2015).

Overall, the meta-analysis suggests that the flipped classroom model increases student learning outcomes over the traditional classroom. This is regardless of class size (>100 vs. <100 students) or of the field of study of the students (social science vs. majors that require mathematics). The one factor that did affect the outcome was the use of quizzes. Ten of the studies used quizzes within the flipped classroom, but only four also used quizzes in the traditional class. Those that had a quiz for both classes had “no statistically discernible difference on performance” between the traditional and flipped classrooms.  

Implications for the Math Classroom

The flipped classroom has some clear advantages by design with readily available online access to content and time in class for practice and application. This meta-analysis of studies comparing undergraduate introductory statistics courses supports the idea that students have increased exam scores and course grades when engaged in a flipped classroom rather than traditional lecture classroom design. However, some questions still remain.

The biggest question is in the use of quizzes. Many online video lectures in a flipped classroom are followed by content quizzes ensuring students have engaged in the video and have learned the content. Traditional in-person lectures do not often employ similar quizzes. When quizzes are used in both the flipped and traditional classrooms, the advantage of the flipped classroom on learning outcomes is diminished. Therefore, it may be that using quizzes could yield better student outcomes, regardless of the classroom format (see Brown, M.J., & Tallon, J., 2015)

Another question is what happens in the face-to-face class meeting. With the flipped classroom, the assumption is that students are almost exclusively engaged in active learning strategies like group work, problem solving, and assignments and that there is peer and instructor support during this in-class time. The assumption with the traditional classroom is that students are passively learning content by listening to a lecture, not engaged in active learning. This may or may not be the case. Details of in class activities within each model would need to be compared and such details are not often described in published studies.  

Time of exposure to content is another consideration. With the flipped classroom, it is the responsibility of the student to engage in the online content. In a traditional class, students are forced to attend for a specific amount of time. There could be a difference in exposure time between the traditional and flipped classroom that is out of the instructor’s control. Depending on how the course is set up, students may spend more or less time in the flipped classroom. Indeed, meta-analysis across different subjects indicates that time of exposure to content is a primary factor for the success of the flipped classroom (see the Teaching newsletter from 11/10/22 for a summary of the published meta-analysis). 

Because of these existing questions, we need to carefully consider whether it is worth converting an introductory statistics course to a flipped classroom design. It may be more worthwhile to make targeted improvements to the traditional classroom in order to improve student outcomes.

How to Implement in the Math Classroom

It takes considerable time to prepare quality video lectures that can be used for a flipped classroom. Ideally, the lectures are short (15 minutes or less) and based on a single simple topic with clearly communicated learning outcomes (“What you should learn from this lecture is…”). It may be worth the time to create a couple of videos or screencasts on topics that are the most challenging.  The videos can then be used as supplements to a traditional class or for occasional flipping. Over time, you can grow the collection of videos that students can use to access content.  

Given the results of the meta-analysis, it may be more valuable to create a couple of short quizzes for content topics rather than videos. These quizzes can be used after the online video lecture or during an in person class. Indeed, administering quizzes before a lecture has been shown to reduce test anxiety and improve performance in a statistics course (Brown and Tallon, 2015). These quizzes could mimic exam questions and thereby help students to have less anxiety about exams. It could also help students identify the important concepts they should be learning from the lecture.

Regardless of whether you use video lectures or quizzes, consider what you are doing with your in class time. Active learning strategies have been shown to improve student learning outcomes (see this example from a Harvard physics class). What kinds of active learning strategies are you currently using and how effective are they with engaging students in learning? Future blogs will explore the research behind some of these strategies and how they affect the college math classroom. 

In summary, the flipped classroom appears to be a promising instructional model, as this meta-analysis shows. But, before taking the time to jump in with both feet and flipping all your content, try making a few targeted video lectures for students. Better yet, create a couple of quizzes to give to students and consider using active learning strategies in the classroom.